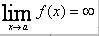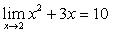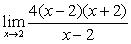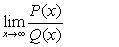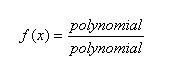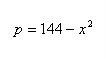Chapter 3.2
Product and Quotient Rules
This section covers two new rules to make finding the derivative easier. The product rule will help us find the derivative of a long function, and the quotient rule will help us find the derivative of the quotient of two functions.
The Product Rule:
d/d(x) [ f(x) g(x) ] = f(x) g'(x) + g(x) f'(x)
The Derivative of the product of two functions is equal to the first function times the derivative of the second function plus the second function times the derivative of the first function.
The Product Rule is very useful for extremely long functions when using 4-step process to find the function will take too much time. So for shorter equations such as x^2, use the 4-step process or the four basic rules for the derivative.
Example of Product Rule:
Find the derivative of f(x) = (7x^3+3x^2+4x-10) (8x^3-4x^2+3x).
f'(x) = (7x^3 + 3x^2+4x-10) (24x^2-8x+3) + (8x^3-4x^2+3x) (21x^2+6x +4)*
*Note: You are able to leave the function unfactored, so you don't have to simplify.
The Quotient Rule
d/d(x) [f(x)/g(x)] = [g(x) f'(x) - f(x) g'(x)] / [g(x)]^2
The derivative of the quotient of two function is equal to the denominator multiplied by the derivative of the numerator minus the numerator times the derivative of the denominator all divided by the square of the denominator.
h(x) = Hi / Lo
"The derivative is equal to LoDHi minus HiDlo divided by what is squared down below."
Example of Quotient Rule:
f(x) = X / (x^2 +1)
f'(x) = {(x^2+1)(1)-[(x) (2x)]} / (x^2+1)^2 which reduces to (1-x^2) / (x^2+1)^2*
* Note: You are able to leave the function unfactored, so you don't have to simplify.
Links for More Assistance:
http://www.mathwords.com/p/product_rule.htm
http://www.mathwords.com/q/quotient_rule.htm
http://en.wikipedia.org/wiki/Product_rule
http://en.wikipedia.org/wiki/Quotient_rule
http://mathworld.wolfram.com/ProductRule.html
http://mathworld.wolfram.com/QuotientRule.html
Next for Wednesday November 11 2006 is Danica on Chapter 3.3, The Chain Rule.
Personalization:
Theorem: 1=2
Proof:
let A=1
let B=A
multiply both sides of (2.) by A, you get AB=A2
subtract B2 from both sides, you get AB-B2=A2-B2
factor left and right hand sides, you get B(A-B)=(A-B)(A+B)
divide both sides by (A-B), you get B=A+B
plug A=1 and B=A into (6.), you get 1=2
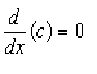


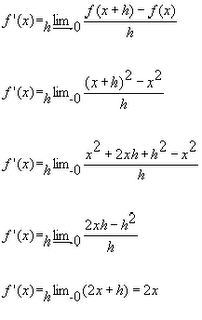





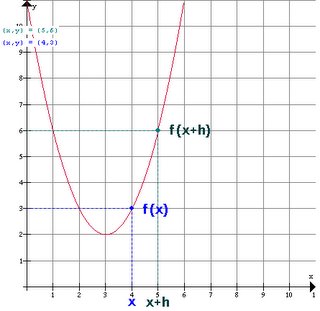

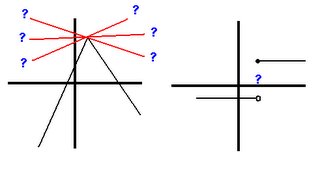


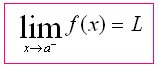


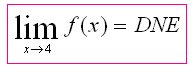



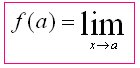






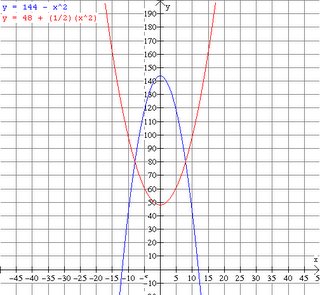
 if the value f(x) can be made as close to the # L as we please by taking x sufficiently close to (but not equal to) a. This means that the limit is the number you are approaching as x gets closer to a.
if the value f(x) can be made as close to the # L as we please by taking x sufficiently close to (but not equal to) a. This means that the limit is the number you are approaching as x gets closer to a.