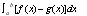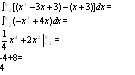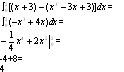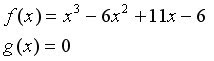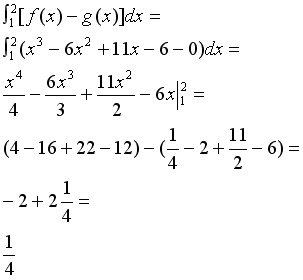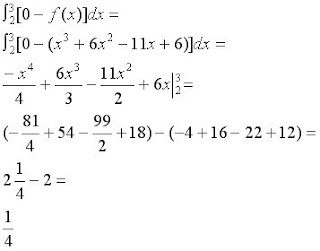Integrals in Business

In the world of business, integrals are used to determine many numbers that may mean the success or the failure of a company.

With integrals and some statistics, we as the CEO's of companies can determine the consumer surplus, the producer surplus, and the market price

where P is the price, and x is the amount of products, the following graphs portray the relationships between price and goods.

for consumer surplus:
The Producer Surplus:
The Marketing Price curve:

A sample problem: given the following information find the producer surplus
Pd = D(x) = -.001x^2 + 250
Ps = S(x) = .0006x^2 + .02x + 100
x = 300
P = 160


PS =


on your calculator: you should put the equation in the parenthesis in the Y1 function and input fnInt(Y1,x,0,300) and you will get a number: 36300 which is the producer surplus because we used the producer surplus function as the Y1.

Future and present value of an Income Stream:
T = time frame
R(t) = rate of income generated
r = Interest rate for reinvestment
this tells you how much you would have if you put your money in a bank and had interest on top of reinvestment.

Present Value function: which is the exact value of the money at the moment is described by
and the Amount Annuity is the future output of your investment and is described by functions
m: payments per year P : amount of payment

Lorentz Curve: Income Distribution
f(x) = proportion of the total income recieved by the poorest 100x% of the population
Domain: [0,1] f(0) = 0 <- if nobody is counted, nobody has money.
Range: [0,1] f(1) = 1 <- if everybody is counted all the money is in one way or another, distributed.

the proportions are shown in between the two extremes of nobody and everybody.

It is always increasing because a person's income cannot be negative.

the GINI index which shows the coefficient of the inequality is
some more reference is here

Thou art next DANICA

Chapter 6

Section 6
Area Between Two Curves

We have been able to find the area between the graph and the x-axis, but now we will be able to find the area between two graphs on a given interval (a,b). The concept is pretty easy, it just takes a lot of practice. Please note that a major part of this chapter that must be noticed is the concept that the area is based off of the bottom function subtracted from the top function. This is the reason why we must graph the functions or determine through mathematics which function is the correct top function.

There is just 1 concept we must learn, and simply practice it over and over until its correctly performed quite easily.

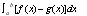
The above equation helps us find the area between the curves, if f(x) is the above function in the area and bounded on the bottom by g(x).
The net area between the functions will always be positive! Due to the fact before, we were dealing with finding the area underneath the graph and above the x-axis, we were able to have a negative area. However, we will always have a positive area between two curves.
If the graph allows for the opportunity for symmetry, use it, it will save you a great deal of work. Like the below example:
F(x)=x^3-3x+3 and g(x)=x+3
First Step: Graph the function:

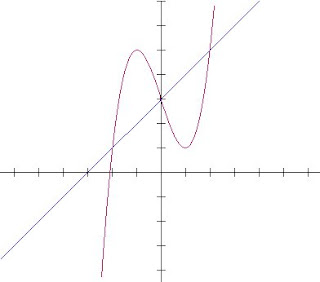
Second Step: Set the two functions equal to each other, in order to find the points of intersection of the two graphs
x^3-3x+3=x+3
X^3-4x=0
x(x^2-4)=0
x(x+2)(x-2)=0
so the points of intersection occur at x=0,2,-2. By looking at the graph, we see the area we are trying to find occurs in (-2,0) and (0,2)
Note: you are not able to combine the area to make (-2,2), because that is describing a different area, compared to the area we actually want. Also, since we want the area, using the top function, which is the cubic function, so we must take the linear function and subtract it from the cubic function.

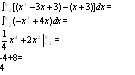
The result of 4 describes the area from (-2,0), but we still need the area from (0,2), however due to symmetry, we know the areas are equal, so by multiplying the 4 by 2, we find the net area between the two graphs to be 8. I also showed this is equal to writing it out longhand and ignoring the symmetry.

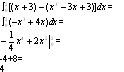
The answer given describes the area between the two curves from (0,2), which is 4. By adding the two areas, we find that 4+4=8, which is the net area between f(x) and
g(x). Note: this is also equal to the first area multiplied by two, since the function is symmetric.

Another Example: Find the area between the curves of the following functions:


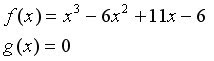
To find the points of intersection, set the two functions equal to each other, and you find the points of intersection are: 1,2,3. The areas of the graph we want to find are from (1,2) and from (2,3). We find the area from (1,2) first, see below for work. Since from (1,2), the cubic function lies above g(x), we subtract g(x) from the cubic function.

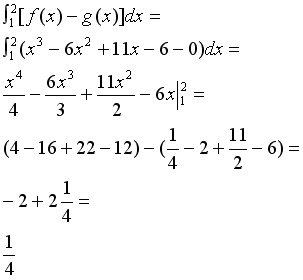
Then we find the area from (2,3) Since from (2,3), the cubic function lies below the graph of g(x), we subtract the cubic function from the function g(x). See below for work.

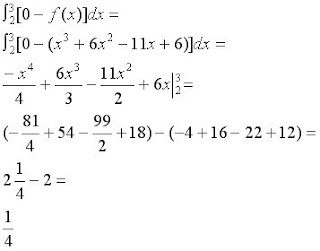
We then add (1/4)+(1/4)=(1/2)
So the net area between the two graphs is 1/2.
Note: we could have used the symmetry law also, but the work was done to show the problem.
Here are some external links which can prove helpful.
http://www.karlscalculus.org/calc12_3.html





Reminder:
KYONG! You're up next for Chapter 6-7 Applications of the Definite Integral to Business and Economics on Thursday March 22, 2007.

Personalization:
Here's a couple quotes to help get you guys through the week:

My life has been full of terrible misfortunes most of which never happened.
- Michel de Montaigne

The way to gain a good reputation, is to endeavor to be what you desire to appear.
– Socrates

When one door of happiness closes, another opens, but often we look so long at the closed door that we do not see the one that has been opened for us.
- Helen Keller

There is always room at the top.
- Daniel Webster

Thursday's Quiz Topics

Here’s a list of topics that will be covered on Thursday’s 6.1-4 Quiz

Quiz Topics - 6.1-4
Indefinite integral – substitution (trig functions)
Area under a trig function (special angles!)
Area approximation – data table
Determine original function f given slope and point
Indefinite integral – substitution (natural log)
Definite Integral – special circumstances
Indefinite integral – substitution (natural logs and exponentials)
Indefinite integral – substitution (trig functions and natural logs)
Area approximation – Midpoints
Definite Integral – geometric
Antiderivative – polynomial
Antiderivative – fractional powers
Antiderivative – position/velocity/acceleration
Area approximation – Right endpoints
Definite Integral – geometric
Definite Integral – polynomial
Definite Integral – fractional powers
Definite Integral – trig function
Indefinite Integral – substitution (fractional exponents)
Indefinite Integral substitution (polynomial)

That’s it! I’ll be in early on Thursday!…

I like nonsense, it wakes up the brain cells. Fantasy is a necessary ingredient in living, It's a way of looking at life through the wrong end of a telescope. Which is what I do, And that enables you to laugh at life's realities.
- Dr. Seuss

I thought this was cute...

Some links for section 6.3

Hi Gang!
Once again, sorry I won’t be around for class. Hopefully the reading isn’t too confusing. To help you out, here are a couple of links to posts your classmates in AB Calculus created when they covered the topics of Area and the definite integral earlier this year. If they make sense, be sure to thank them. If they don’t, ask them questions!

I’m hoping to be back on Friday, but this cough of mine has to go away first. However, I can still answer emails!

Section B:
Laurie L.:
AREAS and DISTANCES

Kristin H.:
DEFINITE INTEGRAL

Section C:
Kane O.:
AREAS and DISTANCES

Claire C.:
DEFINITE INTEGRAL

“That which does not kill us makes us stronger.” – Friedrich Nietzsche (or at least I hope so…)

And here’s a link someone sent me that’s just darn cute:
Instructions for properly hugging a baby.