Section 2.6

Derivative:

Slope of the tangent line

Instantaneous rate of change

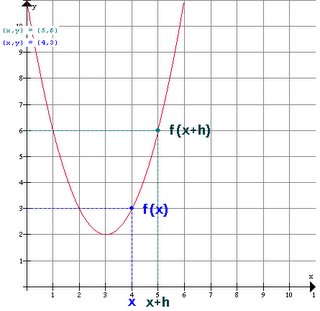
Step 1: f(x) = x² + 5x

f(x + h) = (x + h)² + 5(x + h)

= x² + 2xh + h² + 5x + 5h

The Slope Formula:
f(x + h) – f(x)
x + h – x

Step 2: [(x² + 2xh + h² + 5x) – (x² + 5x)] / h

Step 3:
(2xh + h² +5h) / h
lim h à 0
Step 4:
2x +h + 5 = 2x + 5 make the h = 0 because the limit of h is 0
lim h --> 0

Tip: You must put the equation of the line tangent to the chosen point in point-slope formula or the slope intercept form.

i.e. if according to our step 4, f(3) = 11 you will put it in:

Point Slope: y – 24 = 11(x – 3)

Slope Intercept: y = 11x – 33 + 24 = 11x – 9

Since at the time of the development of Calculus many different mathematicians from different countries found it at the same time, there are many different notations that mean essentially the same thing.

i.e. f¹(x), y¹, dy/dx, Dx(y), Dxf(x)

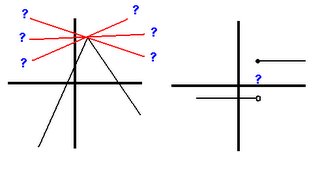
Differentiability

Many functions have derivatives, but some functions have areas where you

cannot draw a tangent line.

i.e.

When the graph of a function has a derivative at a point or interval, it is said to be differentiable

Hint: Differentiability implies continuity

Examples
To find the average rate of change:

Essentially step two above with numbers in place of the variables

For f(t) = 2t² what is the average velocity of [22,23] seconds?

f(23sec) = 1058ft f(22sec) = 968ft

(1058 – 968) / (23 – 22) = 90 / 1 = 90 ft/sec

To find the instantaneous rate of change:

Essentially the entire 4 step process with numbers in place of the variables

For the same f(t) what is the instantaneous velocity at [22] seconds?

f(t + h) = 2(t + h)²

= 2(t² + 2th + h²)

= 2t² + 2th + 2h²

(2t² + 4th + 2h² – 2t²) / h = 4t +2h = 4t

lim h --> 0

[22sec] --> 4t = 88 ft/sec

for Extra assistance visit http://tutorial.math.lamar.edu/AllBrowsers/2413/Differentials.asp

Victim for next Lesson : Drew Titus