2.3: Functions and Mathematical Models

The Four Steps of Solving Word Problems:
1: FORMULATE - you must convert the problem into math language. eliminate extraneous information and pull out the information that will help you solve the problem
2: SOLVE - find an answer by plugging in information in the problem to equations you made in step one
3: INTERPRET - figure out what that number you solved for means
4: TEST - determine whether or not your number make sense in the circumstances of the problem

Rational Functions:
Just as rational numbers can also be expressed as fractions, so too can rational functions.

rational function f(x):






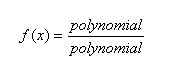
Special Cases (Economics):
Profit is Revenue minus Cost.
Revenue is Price(Retail) times Quantity.
Cost is Price(Wholesale) times Quantity plus any Fixed Costs.

demand equation f(x) = price








supply equation f(x) = price










The intersection of these graphs is economic equilibrium, when supply equals demand.











Sample Problem:

The Rigerbird portable light company has determined their weekly supply and demand equations to be




and




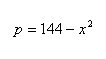
respectively, where p is measured in dollars and x is measured in units of 100. What is the equilibrium quantity and price?

First, we recognize that the equilibrium is the intersection of the graphs. So, we solve for that intersection. We can graph both equations on the same axes so we can see it.



















Then, we can use the intersect function on our calculators to determine that the two points of intersection are (-8, 80) and (8, 80). These answers would mean -800 portable lights per week at $80 and 800 portabel lights per week at $80, respectively. Only one of these answers would make sense in the problem, the second answer, because you cannot phsyically sell -800 portable lights in a week, as the first answer suggests. So, the answer to this problem is 800 lights per week, sold at $80 per light.


Links:
http://en.wikipedia.org/wiki/Supply_and_demand
http://www.netmba.com/econ/micro/supply-demand/

Nicole, you're up next!


"Giving up is the easiest thing you could ever do, but holding it all together when everyone expects you to crumble, now that is true strength."