12.4 Integration of Trigonometric Functions

Finding the Antiderivatives of Trigonometric Functions

Finding the antiderivatives of Trigonometric functions is quite simple. For such problems, you must use (and memorize) the following Integration Formulas:


Some problems may require other formulas such as the following, but you will not be required to memorize them.


Also, if you come across a problem that looks like this:

1. Find the antiderivative


2. Plug in the top number to the antiderivative


3. Plug in the bottom number to the antiderivative


4. Use your answers from steps two and three and find the difference
   
   

Example Problem

Question

Evaluate the following integral.

Solution

Step One: Find the antiderivative.

Step Two: Plug in the the top number to the antiderivative.

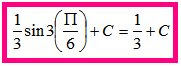
Step Three: Plug in the bottom number to the antiderivative.

Step Four: Find the difference.

Helpful Websites

http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/trigintdirectory/TrigInt.html

http://people.hofstra.edu/faculty/Stefan_Waner/trig/trig4.html

Brian you are up next!

"Sooner or later we all discover that the important moments in life are not the advertised ones, not the birthdays, the graduations, the weddings, not the great goals achieved. The real milestones are less prepossessing. They come to the door of memory."

-Susan B. Anthony

6.1 Antiderivatives

Antiderivatives!!
If we are given a derivative, how do we find the original function

A function F is an antiderivative of f if F'(x) = f(x)
...in other words the derivative of your integral equals the original function

Basic Rules

1. The Antiderivative of a Constant k

2. The Power Rule


3. The Antiderivative of a Multiple of a Function

4. The Sum Rule


5. The Antiderivatice of the Exponential Function

6. The Antiderivative of f(x)= 1/x

You can also find the value of C when given an integral and a point.

Initial Value Problem

Example:

plug in your point


therefore...

Helpful websites:

• http://www.calc101.com/webMathematica/integrals.jsp
• this one actually can help you check your homework answers

• http://archives.math.utk.edu/visual.calculus/4/antider.1/
• http://people.hofstra.edu/faculty/Stefan_Waner/RealWorld/tutorials4/frames6_1.html
  

NICOLE!!!! You're up next :)

“To achieve great things, two things are needed; a plan, and not quite enough time.”
-Leonard Bernstein

Monday's Test Topics

Here’s a list of topics that will be covered on this Monday’s Chapter 4 Test

Chapter 4 Test Topics
Increasing/Decreasing Intervals
Interpret information about the original function from the graph of the derivative
Interpret the meaning of first and/or second derivatives in applications
Determine increasing/decreasing intervals, local extrema, concavity and point(s) of inflection given a function
Sketch a graph of a function given conditions about local and absolute extrema
Find absolute extrema
Determine conditions necessary for points of inflection
Match graphs to first and second derivatives
Optimization problems

That’s it! I’ll be in early on Monday, and available after school today…

At New York's Kennedy Airport today, an individual, later discovered to be a public school teacher, was arrested trying to board a flight while in possession of a ruler, a protractor, a set square, and a calculator. Attorney General John Ashcroft believes the man is a member of the notorious Al-Gebra movement. He is being charged with carrying weapons of math instruction.
Al-Gebra is a very fearsome cult, indeed.They desire average solutions by means and extremes, and sometimes go off on a tangent in a search of absolute value. They consist of quite shadowy figures, with names like "x" and "y", and, although they are frequently referred to as "unknowns", we know they really belong to a common denominator and are part of the axis of medieval with coordinates in every country. As the great Greek philanderer Isosceles used to say, there are 3 sides to every angle, and if God had wanted us to have better weapons of math instruction, He would have given us more fingers and toes.
Therefore, I'm extremely grateful that our government has given us a sine that it is intent on protracting us from these math-dogs who are so willing to disintegrate us with calculus disregard.
These statistic bastards love to inflict plane on every sphere of influence. Under the circumferences, it's time we differentiated their root, made our point, and drew the line. These weapons of math instruction have the potential to decimal everything in their math on a scalar never before seen unless we become exponents of a Higher Power and begin to appreciate the random facts of vertex.
As our Great Leader would say, "Read my ellipse". Here is one principle he is uncertainty of---though they continue to multiply, their days are numbered and sooner or later the hypotenuse will tighten around their necks.

4.5 Optimization II

Optimization Word Problems
In this section we are learning to apply our knowledge of optimization (section 4.4) in everyday life.

Steps in solving an optimization word problem:
1. Draw a picture.
2. Determine what you are maximizing and minimizing.
3. Find the constraints
4. Use constraints to rewrite the equation.
5. Find the derivative of the equation.
6. Find the zeros.
7. Test your answer to make sure it is correct.

EXAMPLE PROBLEM:
A father is planning to construct a large rectangular sand box for his kids. He has a total of 38 feet of wood to outline the edges of the box. Find the dimensions for the largest sand box he can create if he uses all of the wood.

SOLUTION:

1. Draw a picture.

2. Determine what you are maximizing or minimizing.

I am maximizing the Area.

3-4. Find the constraints, and using constraints rewrite your equation.

We only have 38 feet of wood available.

5. Find the derivative of the new equation.

6. Find the zeros

7. Test it

If the width is 9.5 and we have 2 widths and 2 lengths to add together than we can conclude that:

In conclusion: The dimensions of the rectangle, which actually seemed to be a square are 9.5 feet by 9.5 feet.

ANSWER:

9.5 feet by 9.5 feet

OTHER SOURCES:

http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/maxmindirectory/MaxMin.html

http://math.dartmouth.edu/~klbooksite/3.06/306.html

This one is interesting. It has to do with optimization in marketing:

http://www.lindo.com/library/advertap.pdf

KATELYN!!!! you are up next. :)

If you are completely frustrated with these problems don't be worried. It takes practice, and I mean a lot of practice.

"It is not work that kills men, it is worry. Work is healthy; you can hardly put more on a man than he can bear. But worry is rust upon the blade. It is not movement that destroys the machinery, but friction."

-Henry Ward Beecher

4.4 Optimization I

Optimization
Optimization is the process of finding the ABSOLUTE extrema in a given interval.



















The absolute maximimum and minimum are the largest and smallest y-values, respectively, within the interval. As seen in the picture, the absolute mimimum is the lowest point on the graph and the absolute minimum is the highest point on the graph.

At a given point "c":
If f(c) is the smallest value of f(x), then the point (c, f(c)) is the absolute minimum.
If f(c) is the largest value of f(x), then the point (c, f(c)) is the absolute maximum.

3 Steps to Finding Absolute Extrema
1. Find the critical points of f(x) that are within the given interval (a,b)
2. Compute the f(x) values for each of the critical points AND f(a) and f(b)
3. The point with the largest f(x) value is the absolute maximum and the point with the smallest f(x) value is the absolute minimum

Sample Problem:
Find the absolute extrema of the function on the interval [0,6]:



ANSWER:
In order to find the critical points we must use the derivative of the function and find its zeros. The zeros are -1.09 and .76, but because -1.09 is not within the interval, that number is discarded. Then we plug .76, 0, and 6 into the original equation. Once we find those values for f(x), we determine the absolute minimum and maximum.
















We find that the absolute maximum is at the point (6, 439) and the absolue minimum is at the point (.76, -1.34).

Another source for Optimization:
http://tutorial.math.lamar.edu/AllBrowsers/2413/AbsExtrema.asp

KJ, you're up next.

After that last quiz, I have a good quote for everyone:
"Don't worry about your difficulties in mathematics. I assure you mine are greater." - Albert Einstein

Wednesday's Quiz Topics

Here’s a list of topics that will be covered on Wednesday’s 4.1-3 Quiz

Quiz 4.1-3 Topics
Find critical numbers of a function.
Find increasing/decreasing intervals.
Find inflection points.
Identify characteristics of a function given the graph of the derivative of the function and sketch the function.
Find the coefficients of a cubic function given local minimum and maximum values.
Determine coefficients of a function given information about points of inflection.
Match the graph of a function to first and second derivative conditions.
Determine key characteristics of a function (increasing/decreasing, local max/min, concavity and inflection points)

That’s it! I’ll be in early on Wednesday… and Happy Valentine's Day!

It’s kind of fun to do the impossible. – Walt Disney

4.2 Concavity

Concave up - All tangent lines are below a curved graph
Concave Down - All tangent lines are above a curved graph

You can tell whether a graph is concave up or down by looking at its second derivative:
f''(x) is Positive(+), the graph is concave up and its slope increases
f''(x) is Negative(-), the graph is concave down and its slope decreases

Point of Inflection:
When the concavity of a graph changes

to find where the graph is concave up and where it is concave down, you may use
The Number Line Test:
in the number line test, you find the point of inflection, then you plug in numbers that are larger or smaller than the x value in the point of inflection to find the correct signs to use the rule above.

ie. y=x^5
y'=5x^4
y''=20x^3
Now, you must make the y=0 to find the point of inflection, so if you do that, the x must equal 0 to make the y value also equal 0.
that is our point of inflection (0,0)
so we start to plug in numbers like 1 and -1 which are larger than 0 and smaller than 0
the results we get are for 1 and -1 are 20 and -20 respectively. and since, 1 results in a positive number, we can say, by using the rule, that the right side of 0 must be concave up and vice versa for the negative .

Maximums and Minimums:
If the second derivative is positive, we get a minimum
If the second derivative is a negative, we get a maximum

ie.
f(x)=x^3-3x^2-24x+32

f'(x)=3x^2-6x-24=0
3(x^2-2x-8)=0
3(x-4)(x+2)=0 x=4,-2

f''(x)=6x-6
for values 4 and -2 plugged into the second derivative equation, we get for 4, positive value which indicates a minimum, and for -2, a negative value which indicates a maximum.

for additional reference go here --> here--> no, here
"As long as Calculus is taught in school, there will be prayer in school."

Graphing rational functions is a pain in the asymptote.

This isn't really a joke, it supposedly happened in a UK GCSE exam some years ago, but it may amuse you:
Q: how many times can you subtract 7 from 83, and what is left afterwards?
A: I can subtract it as many times as I want, and it leaves 76 every time.

Danica Thou Art Next!

Second Semester Posting Order and Reminder

Since Blogger decided to add its "new and improved" feature - scrambling the order of the blog contributors, we need to finalize the posting order. So here we have it (based on the last list we viewed in class):



Brian
Kyong
Danica
Drew
Kjirsten
Katelyn
Nicole





Ok. Thanks for all your great work on this blog - it's been a great experience so far. Keep it up!
And don't forget - your first chapter of your calculus novel is due on Monday. Submit your final PowerPoint presentation to our class website (final submissions) Use the format: CSPCH1-Group1.ppt

Group 1: Nicole/Drew
Group 2: Kyong/Brian
Group 3: Kjirsten/Katelyn/Danica

Have a great weekend!



In order to attain the impossible, one must attempt the absurd.
- Miguel de Cervantes
(of course, that happens regularly in our class!)





Poor study strategies:

Chapter 4-1

Applications of the First Derivative

Vocabulary:

relative maximum- for a function f, the relative maximum occurs at x=c if there exists an open interval (a,b) containing c such that f(x)≤f(c) for all x in (a,b)

relative minimum- for a function f, the relative minimum occurs at x=c if there exists an open interval (a,b) containing c such that f(x) ≥f(c) for all x in (a,b)

Notes:

If two points exist, and y2>y1 then the function is increasing

If two points exist, and y2

For the derivative:

If f'(x) >0 then the function is increasing... If the tangent line has a positive slope, then the function is increasing.

If f'(x)<0>

A relative maximum or minimum is the maximum or minimum point in a "neighborhood."

At a critical point, the derivative of the function is either equal to zero or is undefined at point c. Maximum and Minimum points will only occur at a critical point.
At the relative maximum or minimum, the derivative is equal to ZERO or when the derivative is UNDEFINED.

If a relative maximum or minimum does exist, the one of the above not necessarily both MUST be true.

The First Derivative Test

The first derivative test is used to see if a point f(c) is a relative maximum or minimum.

If f'(x)>0 for xc then f(c) is a relative maximum.

If f'(x)<0>0 for x>c then f(c) is a relative minimum.

For the first derivative test, it is always helpful to make a sign chart and find where the graph is increasing and decreasing around the point c. This chart allows you to see if the point is a relative maximum or minimum.

Several Questions can be phrased different ways about the first derivative:

At what x-values do relative maximum and minimum points occur?

For the above, you simply have to list the values of x.

What are the values at the relative maximum and minimum points?

For the above, the question is asking for the value, which refers to the value of y at x. In order to find the value, simply plug in the x-values into your original equation (not the derivative equation) and find the y-value. Only give the y-value.... not the x and y value!

What are the coordinates at the relative maximum and minimum points?

For the above, you are looking for the points, so you plug the x-values back into your original equation, and pair that answer with the x-value to make a point. This point should reflect where the maximum or minimum point occurs.

When is the graph increasing?

For the above, you should make a sign chart! Where the sign chart shows positive numbers, the graph is increasing. Where the sign chart shows negative numbers that decrease, the graph is decreasing.

SOME EXCEPTIONS DO OCCUR:

The horizontal tangent line does fit the rule of having the derivative equal zero or be undefined, but there is no maximum or minimum point.

The derivative does not exist, but a relative minimum does exist. It is not differentiable at x=0, but the relative minimum does occur there.

Example: What are x-values for the relative maximum and minimum points in the following function:

Take the derivative to find that the derivative equation is:

You can factor out the 2 to get 2(x+7)(x-5). Set that equal to zero and find that x=-7 and x=5. Make a sign chart to find that the graph is increasing from negative infinite to -7 and decreases from -7 to 5. So we can establish that the point at x = -7 is a maximum. And by making a sign chart we find that that the graph is decreasing from -7 to 5 and that it increases from 5 to infinite. So we can establish that x = 5 is a minimum.

X= -7 is a maximum and x=5 is a minimum.

Supportive External Link:

http://www.aspire.cs.uah.edu/textbook/method003.html

http://www.math.uh.edu/~mmarksc/Webpage%20Spring%202006/Lesson%2010.pdf

http://www.math.uh.edu/~beatrice/1314%20L10.pdf

Next for the Blog is Kjirsten for Chapter 4.2 Applications of the Second Derivative on February, Wednesday 7 2007.

Personalization: Valentine's Day is in only 8 days!