2.4 Limits
Expressing Limits
The function F has the limit L as x approaches a, written
 if the value f(x) can be made as close to the # L as we please by taking x sufficiently close to (but not equal to) a. This means that the limit is the number you are approaching as x gets closer to a.
if the value f(x) can be made as close to the # L as we please by taking x sufficiently close to (but not equal to) a. This means that the limit is the number you are approaching as x gets closer to a.(The Limit as X approaches a of F(x) is L)
If the equation had a hole where L is the limit would still be the same.
.
(Infinite Limit is true by both sides, increasing without bounds.)
DNE = Does not exist
Your fingers do not meet when tracing.
BUT if you are looking for  or
or  it is possible.
it is possible.
Positive and negative signs indicate direction. Positive = traveling from right to left and Negative = traveling from left to right.
In this case the limits would be:
Evaluating Limits
Direct Substitution
To find the limit without looking at a graph. I plugged in 2 for the equation. 2 squared plus 6 equals 10. 10 is the limit as x approaches 2.
If you have a hole in your graph than you want to try and see the removable discontinuity.
transforms to transforms to

now you can plug in 2 for the equation 4(x+2).
The limit is 16. The limit of 4(x+2) as x approaches 2 is 16.
Limits at Infinity
Rules:
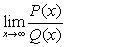
1. If the degree of P(x) is greater than the degree of Q(x) , then the limit will be + or - infinity.
2. If the degree of P(x) is less than the degree of Q(x), then the limit will be a horizontal asympotote at 0.
3. If the degree's of the function are a tie than there will be a horizontal asymptote at the ratio of the leading coefficients.
Example Problem

What is the limit of the function as x approaches infinity?
The function has the same degrees on both top and bottum. You can use the infinity rule that the degree's of the function are a tie. Because they are a tie, this means that the limit is a horizontal asymptote at the ratio of the leading coefficients. In this case the ratio is 17/7.
ANSWER: 17/7
some extra sites on limits:
http://www.coolmath.com/limit1.htm
http://www.calculus-help.com/funstuff/phobe.html
http://curvebank.calstatela.edu/limit/limit.htm
Reminder:
hey nicole....you are up next!
Since it is almost halloween here is a cute joke:
Q: What do you get if you divide the cirucmference of a jack-o-lantern by its diameter?
A: Pumpkin Pi!


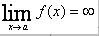




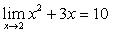

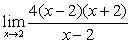

1 Comments:
I like your first link. I was absent on the day of the lesson, so I was very lost on the concept of limits. The geometric example was an odd but effective way to explain the basic definition of a limit. That website explains calculus concepts in a simple way which is also different from the way it is presented to us. It was very helpful!
Post a Comment
<< Home