2.5 One-Sided Limits and Continuity
One-Sided Limits
The function f has the right-hand limit L as x approaches a from the right, written

The function f has the left-hand limit L as x approaches a from the right, written 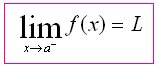
A limit can exist if and only if the one-sided limits agree.
Find the limit, the right-hand limit, and the left-hand limit from this graph.
A Function is Continuous if it satisfies all of the following
1) f(a) exists.
*Remember that a function is continuous if you can trace the entire graph with your finger
Continuous Functions
1) Polynomials
2) Constants
3) Sin and Cos
4) Exponential
5) Logarithmic (on their domain)
Is the function on the graph continuous?
No, because the function is not continuous at x = -2
Intermediate Value Theorem
If f(x) is a continuous function on a closed interval [a, b] and M is any number between f(a) and f(b), then there is at least one number c in [a, b] such that f(c) =M
Existence of Zeros of a Continuous Function
If f is a continuous function on a closed interval [a, b], and if f(a) and f(b) have opposite signs, then there is at least one solution of the equation f(x) = 0 in the interval [a, b] 
Example Problem
Calculate the left and right hand limits of f (x) at 2.
As x approaches 2 from the left, f (x) = 3 - x and f(x) = 1 at x=2 so the left-hand limit is 1
As x approaches 2 from the right f(x) = x/2 and f(x) = 1 at x=2 so the right hand limit is 1.
Here are some helpful links:
http://tutorial.math.lamar.edu/AllBrowsers/2413/Continuity.asp
http://tutorial.math.lamar.edu/AllBrowsers/2413/OneSidedLimits.asp
Kyong you are up next!
"If you see a friend without a smile, give him one of yours"





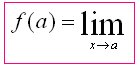




2 Comments:
i definitely have to say that i found the first website to be very helpful for the quiz. It had a really cool graph, and i learned something new with trigonomic functions because it included lim with trigonomic functions. It was most interesting.
Nicole, thank you for the example problem, I used it to help me prepare for the test and I found it very useful to ensure that I understood one-sided limits
Post a Comment
<< Home