7.1 Integration by Parts

Integration by parts is a way to find the integral of 2 functions that are being multiplied together. As we know:




By integrating both sides of the equation, we come up with:




Then, by simple subtraction, we come up with:




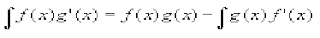Finally, by substituting the following variables, we come to the
Integration by Parts Formula:














By using this formula, we can now do what we already know how to do which is assign variables u and v for funtions to find the integral of a more complicated function.

In order to choose what functions to assign to u and dv, use these guidlines:
1. du is simpler than u
2. dv is easy to integrate

Let's do a Sample Problem:

Evaluate:





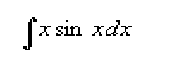
First, assign u and v to their functions and then use the Inegration by Parts Formula to solve the equation.

If you have any trouble, these sites may be able to help you understand a little better:
Good Help
Tough Sample Problems to test your skills

KJ, you are up next with 7.3 Numerical Integration

"Who has not been amazed to learn that the function y = e^x, like a phoenix rising from its own ashes, is its own derivative?" - Francois le Lionnais