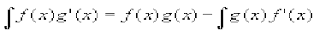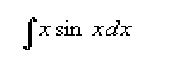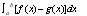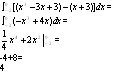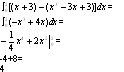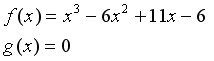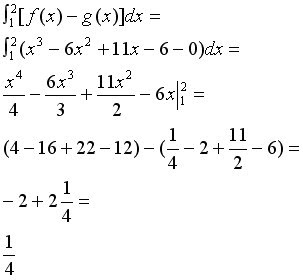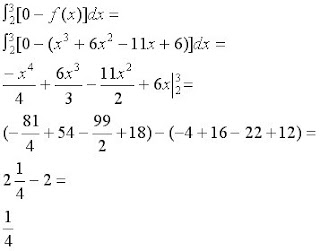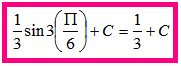Section 6
Area Between Two Curves
We have been able to find the area between the graph and the x-axis, but now we will be able to find the area between two graphs on a given interval (a,b). The concept is pretty easy, it just takes a lot of practice. Please note that a major part of this chapter that must be noticed is the concept that the area is based off of the bottom function subtracted from the top function. This is the reason why we must graph the functions or determine through mathematics which function is the correct top function.
There is just 1 concept we must learn, and simply practice it over and over until its correctly performed quite easily.
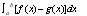
The above equation helps us find the area between the curves, if f(x) is the above function in the area and bounded on the bottom by g(x).
The net area between the functions will always be positive! Due to the fact before, we were dealing with finding the area underneath the graph and above the x-axis, we were able to have a negative area. However, we will always have a positive area between two curves.
If the graph allows for the opportunity for symmetry, use it, it will save you a great deal of work. Like the below example:
F(x)=x^3-3x+3 and g(x)=x+3
First Step: Graph the function:
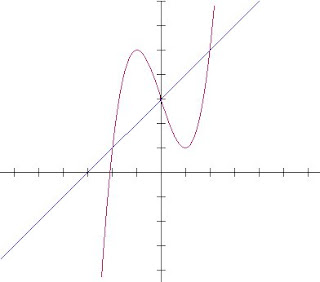
Second Step: Set the two functions equal to each other, in order to find the points of intersection of the two graphs
x^3-3x+3=x+3
X^3-4x=0
x(x^2-4)=0
x(x+2)(x-2)=0
so the points of intersection occur at x=0,2,-2. By looking at the graph, we see the area we are trying to find occurs in (-2,0) and (0,2)
Note: you are not able to combine the area to make (-2,2), because that is describing a different area, compared to the area we actually want. Also, since we want the area, using the top function, which is the cubic function, so we must take the linear function and subtract it from the cubic function.
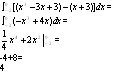
The result of 4 describes the area from (-2,0), but we still need the area from (0,2), however due to symmetry, we know the areas are equal, so by multiplying the 4 by 2, we find the net area between the two graphs to be 8. I also showed this is equal to writing it out longhand and ignoring the symmetry.
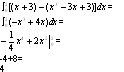
The answer given describes the area between the two curves from (0,2), which is 4. By adding the two areas, we find that 4+4=8, which is the net area between f(x) and
g(x). Note: this is also equal to the first area multiplied by two, since the function is symmetric.
Another Example: Find the area between the curves of the following functions:
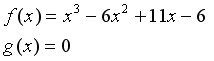
To find the points of intersection, set the two functions equal to each other, and you find the points of intersection are: 1,2,3. The areas of the graph we want to find are from (1,2) and from (2,3). We find the area from (1,2) first, see below for work. Since from (1,2), the cubic function lies above g(x), we subtract g(x) from the cubic function.
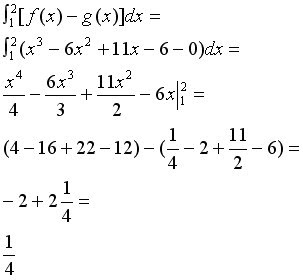
Then we find the area from (2,3) Since from (2,3), the cubic function lies below the graph of g(x), we subtract the cubic function from the function g(x). See below for work.
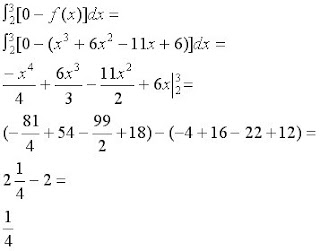
We then add (1/4)+(1/4)=(1/2)
So the net area between the two graphs is 1/2.
Note: we could have used the symmetry law also, but the work was done to show the problem.
Here are some
external links which can prove helpful.
http://www.karlscalculus.org/calc12_3.htmlReminder:
KYONG! You're up next for Chapter 6-7 Applications of the Definite Integral to Business and Economics on Thursday March 22, 2007.
Personalization:
Here's a couple quotes to help get you guys through the week:
My life has been full of terrible misfortunes most of which never happened.
- Michel de Montaigne
The way to gain a good reputation, is to endeavor to be what you desire to appear.
– Socrates
When one door of happiness closes, another opens, but often we look so long at the closed door that we do not see the one that has been opened for us.
- Helen Keller
There is always room at the top.
- Daniel Webster