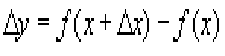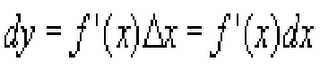Happy New Year!

Happy New Year! I hope you all had a great holiday. Seniors, I hope all those essays were finished. Juniors, I hope you all enjoyed not having to write them (this year!). I spent the last week having a great time up in Oregon with my family, and if you thought it was cold here…

You will notice when you log on to our blogs to creat a post that we have switched over to the “new Blogger.” It’s supposed to make things easier and run smoother (we’ll see!) but it will require each of you to switch over as well (and create a Google account) before you can edit or create new posts. Nothing serious, but I wanted to give you a heads up before your turn came around and you panicked!

See you all on the 8th! Don't forget Bonus Day!

12.3: Differentiation of Trig Functions

Derivatives of the Trigonomic Functions

derivative of sin(x) = cos(x)
derivative of cos(x) = -sin(x)

*We can use these to find the derivatives of the other trig functions which are:

derivative of tan(x) = sec^2(x)
derivative of cot(x) = -csc^2(x)
derivative of sec(x) = sec(x) tan(x)
derivative of csc(x) = -csc(x) cot(x)

Examples

• Find the derivative of sin(7x+3)

• Use the chain rule to find the derivative of the function.

  derivative of the outside function while the inside stays the same times the
  derivative of the inside.

  Answer: cos(7x+3) (7)

• Find the derivative of e^csc(x)

• Follow the steps that we learned in a earlier lesson

  e to the something times the derivative of the
  something

  Answer: (e^csc(x)) (-csc(x) cot(x))

Check out this site for more practice problems:

http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/trigderivdirectory/TrigDerivatives.html

KJ you are up next. I couldn't tell you which one because it is not even on the TWS.

"He who has no Christmas in his heart will never find Christmas under a tree."

Chapter 5-4

Differentiation of Exponential Functions

The following section describes how to find the derivative of an exponential function using the chain rule.

Equations:

Simple Derivative
d/d(x) (e^x) = (e^x)

verbally: the derivative of the function "e" to the "x" is equal to "e" to the "x."

Chain rule:
d/d(x) (e^f(x)) = (e^(f(x)))(f ' (x))

verbally: the derivative of "e" raised to some function f(x) is equal to "e" raised to some function f(x) multiplied by the derivative of f(x).


*Note: do not use the power rule on an exponential function, you can only perform the power rule when "x" is in the base of the function.

Example:
e^(2x+3)
Using the chain rule we find that e^(2x+3) = e^(2x+3) d/dx (2x+3) = e^(2x+3)(2) = 2e^(2x+3)

Other Sources for Differentiation of Exponential Functions:
http://www.tcc.edu/VML/Mth163/documents/DifferentiationofExponentialFunctions.ppt#3
http://www.analyzemath.com/calculus/Differentiation/exponential.html
http://www.lgfl.net/lgfl/leas/sutton/web/Resources/mathematics/Diff%20exp%20fns.xls
http://webpages.charter.net/mgroves9/explogdiff.html

Next for the Blog is Danica for Chapter 5-5 Differentiation of Logarithmic Functions

Personalization:
Top ln(e^10) reasons why e is better than pi.
10) e is easier to spell than pi.
9) pi ~= 3.14 while e ~=2.718281828459045.
8) The character for e can be found on a keyboard, but pi sure can't.
7) Everybody fights for their piece of the pie.
6) ln(pi^1) is a really long number, but ln(e^1) = 1.
5) e is used in calculus while pi is used in baby geometry.
4) 'e' is the most commonly picked vowel in Wheel of Fortune.
3) e stands for Euler's Number, pi doesn't stand for anything.
2) You don't need to know Greek to be able to use e.
1) You can't confuse e with a food product.

3.7 Differentials

Increments:
Increment in x (change in x):





Increment in y (change in y):




Example Problem:
Find the Increment in y as x changes from 3 to 3.01 if f(x)=x^2:



















The Differential:
The differential is a quick and easy way to find the change in y due to a small change in x.
If y=f(x) and is a differentiable function of x, then:
1) The differential dx is:




2) The differential dy is:





Example Problem:
Find the value of the square root of 17.1 using differentials:
Because we know that the square root of 16 is 4, we will find the change in y as x changes from 16 to 17.1. (substitute dy for y', sorry if that wasn't clear)



















We can also use the linear approximation technique:
y=y1+m(x-x1)

To find the error of our approximation, we can use the relative error formula:
dy/y

Error of Last Example Problem:









Some in-depth info about differentials
Some good practice problems

Brian, you're up next with 5.4 Differentiation of Exponential Functions

My 2 Favorite Christmas Jokes:
Q: What do you get when you cross a snowman with a vampire?
A: Frostbite.

Q: What do elves learn in school?
A: The Elf-abet!

Section 3.6

implicit differentiation - a method of solving for finding both x and the y explicitly using only an implicit formula

An implicit formula: ((x^2)+1)y = (x^2) - 1
An explicit Formula: y = f(x) = ((x^2)-1)/((x^2)+)

You can find dy/dx of an Implicit Differentiation
1. by finding the derivatives of both sides of the equation in respect to x. (Any term involving the varible y must involve the factor dy/dx)
2. Solve the result for dy/dx in terms of x and y.

This method of implicit differentiation is for those equations which have an x and a y on one side of the equation and you cannot solve the equation in respect to x.

a simple notes/book example: y^2 = x

(d/dx)(y^2) = (d/dx)(x)
and since y = f(x)
(d/dx)(y^2) = (d/dx)[f(x)]^2 write y = f(x)
= 2f(x)f'(x) Use the Chain Rule
= 2y(dy/dx) Return to using y instead of f(x)
2y(dy/dx) = 1
(dy/dx) = (1/2y)

Related Rates: x and y are a function of a third variable "t"
Up to this point, we have found that the y is moved by the x, but now both x and y are moved by a third variable "t"

we look for both (dx/dt) and (dy/dt) in these related rates.

a cylinder with radius = 3cm
has water flowing into it at 21 cm^3 per minute

the volume formula of the cylinder is V = 9(pi)(height)

(dV/dt) = 9(pi)(dH/dt)
((21cm^3)/1min) = 9(pi)(dH/dt)
((21cm^3)/(9[pi]min)) = (dH/dt)

If in need of more assistance go HERE

GOGOGOGO Drew Titus next BLOG

Some Jokes in Good Taste
New York (CNN). At John F. Kennedy International Airport today, a Caucasian male (later discovered to be a high school mathematics teacher) was arrested trying to board a flight while in possession of a compass, a protractor and a graphing calculator.
According to law enforcement officials, he is believed to have ties to the Al-Gebra network. He will be charged with carrying weapons of math instruction.

Some engineers are trying to measure the height of a flag pole. They only have a measuring tape and are quite frustrated trying to keep the tape along the pole: It falls down all the time.
A mathematician comes along and asks what they are doing. They explain it to him.
"Well, that's easy..."
He pulls the pole out of the ground, lays it down, and measures it easily.
After he has left, one of the engineers says: "That's so typical of these mathematicians! What we need is the height - and he gives us the length!"