3.7 Differentials

Increments:
Increment in x (change in x):





Increment in y (change in y):




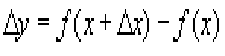
Example Problem:
Find the Increment in y as x changes from 3 to 3.01 if f(x)=x^2:



















The Differential:
The differential is a quick and easy way to find the change in y due to a small change in x.
If y=f(x) and is a differentiable function of x, then:
1) The differential dx is:




2) The differential dy is:





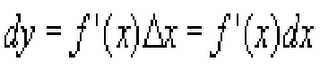
Example Problem:
Find the value of the square root of 17.1 using differentials:
Because we know that the square root of 16 is 4, we will find the change in y as x changes from 16 to 17.1. (substitute dy for y', sorry if that wasn't clear)



















We can also use the linear approximation technique:
y=y1+m(x-x1)

To find the error of our approximation, we can use the relative error formula:
dy/y

Error of Last Example Problem:









Some in-depth info about differentials
Some good practice problems

Brian, you're up next with 5.4 Differentiation of Exponential Functions

My 2 Favorite Christmas Jokes:
Q: What do you get when you cross a snowman with a vampire?
A: Frostbite.

Q: What do elves learn in school?
A: The Elf-abet!