Section 3.3 The Chain Rule

The Chain Rule
The Chain Rule is used to find the derivative of a function with more than one layer.
Let's take the function



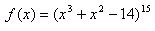
With the tools we have learned over the last couple of days, we would have to expand this function and then use the power rule to find the derivative. Having to expand a polynomial to the 15th power, however, would not be much fun. Instead, why don't we think of the function f(x) as two different functions, g(x) and h(x). Lets set f(x) equal to g(h(x)). How does this help? Well, lets look at how we would seperate f(x) into its components. Lets use the following definitions of g(x) and h(x).






Now we can use the Chain Rule for layered operations. It looks like this:

So, if

and

then



Further Information:
http://archives.math.utk.edu/visual.calculus/2/chain_rule.4/index.html

Next Up: Nicole


"Draw a line and live above it."