3.4 Marginal Functions in Economics

Marginal Analysis

Marginal analysis is the study of the rate of change of economic quantities

So in this lesson MARGINAL is the same as DERIVITIVE OF

Marginal Cost: the derivative of the cost function
Marginal Revenue: the derivative of the revenue equation
Marginal Profit: the derivative of the profit equation

Cost Functions

To find the actual cost of the last individual product produced (x):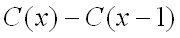

To find the marginal cost of the number of products produced (x):
Find the derivative of the cost function

To find the average cost per unit produced:

Use the notation for the average cost per unit produced: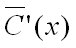

Revenue Functions

To find the revenue:

To find the marginal revenue:

Find the derivative of the revenue function

Profit Functions

To find the profit:

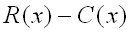
To find the marginal profit:

Find the derivative of the profit function

Elasticity of Demand

To find the elasticity of demand:

Elastic: if (E>1) then an increase in price will cause a decrease in revenue (revenue will react in an opposite manner from the price)

Inelastic: if (E<1)> then an increase in price will cause an increase in revenue (revenue will react in a similar manner as the price)

Unitary: if (E=1) then an increase in price will cause the revenue to stay about the same

Example Problem

Find the elasticity of demand from the demand equation if Sally is selling Prepstock tickets for $12:

Step 1: Resolve the equation in terms of x.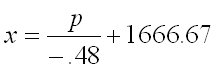 Step 2: Plug in to the elasticity equation

Step 3: Find the elasticity of any price (p), in this case plug in 12

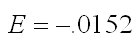
Here is a site with some practice problems:

http://www.math.purdue.edu/~rzhao/Courses/MA223/Lesson17.pdf

KJ, you are up next with lesson 3.5 High Order Derivatives.

"Cherish your vision and your dreams as they are the children of your soul; the blueprints of your ultimate achievements."