5.2: Logarithmic Functions

Formulas and Properties:

Logarithm of x to the Base b:
y = logb(x) if and only if x = b^y (x>0)

Logarithmic Notation:
log(x) = log10(x)
ln(x) = loge(x)

Laws of Logarithms:
logb(mn) = logb(m) + logb(n)
logb(m/n) = logb(m) - logb(n)
logb(m^n) = nlogb(m)
logb(1) = 0
logb(b) = 1

Logarithmic Function:
f(x) = logbx (b>0, b does not = 0)

Properties of the Logarithmic Function:
1. Its domain is (0, infiniti)
2. Its range is (-infiniti, infiniti)
3. Its graph passes through the point (1,0)
4. It is continuous on (0, infiniti)
5. It is increasing on (0, infiniti) if b>1 and decreasing on (0, infiniti) if b<1

Properties Relating e^x and lnx:
e^(lnx) = x (x>0)
ln(e^x) = x (for any real number x)

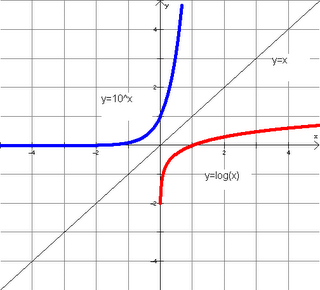
Graph of Logarithms:
A logarithmic function is the inverse of an exponential function. Thus, a logarithmic function is the reflection of an exponential function over the equation y = x:




















Practice Problem:

Q: Simplify the following logarithm:

5log7(x) + log7(7^1) - 2log7(x)






A:
5log7(x) + log7(7^1) - 2log7(x)

log7(x^5) + log7(7) - log7(x^2)

log7[(x^5)/(x^2)] + 1

log7(x^3) + 1



Link to a Logarithm Page

Brian, you're up next and you'll be covering Section 5.3: Compound Interest.

Logarithm Joke:
Question: How do we reduce an exponential growth of grass?
Answer: Using a "ln"-mower!